Test Review Quadratic Equations Word Document Algebra 1

Quadratic Equation

Quadratic equations are second-degree algebraic expressions and are of the class axⁱⁱ + bx + c = 0. The word "Quadratic" is derived from the word "Quad" which means foursquare. In other words, a quadratic equation is an "equation of caste 2." There are many scenarios where a quadratic equation is used. Did y'all know that when a rocket is launched, its path is described by a quadratic equation? Farther, a quadratic equation has numerous applications in physics, engineering, astronomy.

The quadratic equations are 2nd-degree equations in x that have two answers for x. These two answers for ten are also called the roots of the quadratic equations and are designated as (α, β). Nosotros shall learn more about the roots of a quadratic equation in the below content.

1.	What is a Quadratic Equation?
ii.	Quadratic Equation Formula
iii.	Of import Formulas for Solving Quadratic Equations
4.	Roots of a Quadratic Equation
5.	Methods to Solve Quadratic Equations
6.	Quadratic Equations Having Common Roots
7.	Maximum and Minimum Value of Quadratic Expression
eight.	Examples on Quadratic Equation
9.	Practice Questions on Quadratic Equations
10.	FAQs on Quadratic Equations

What is Quadratic Equation?

A quadratic equation is an algebraic expression of the second degree in x. The quadratic equation in its standard form is ax² + bx + c = 0, where a, b are the coefficients, x is the variable, and c is the abiding term. The first condition for an equation to be a quadratic equation is the coefficient of xⁱⁱ is a not-zero term(a ≠0). For writing a quadratic equation in standard form, the x² term is written first, followed by the x term, and finally, the constant term is written. The numeric values of a, b, c are by and large not written as fractions or decimals merely are written as integral values.

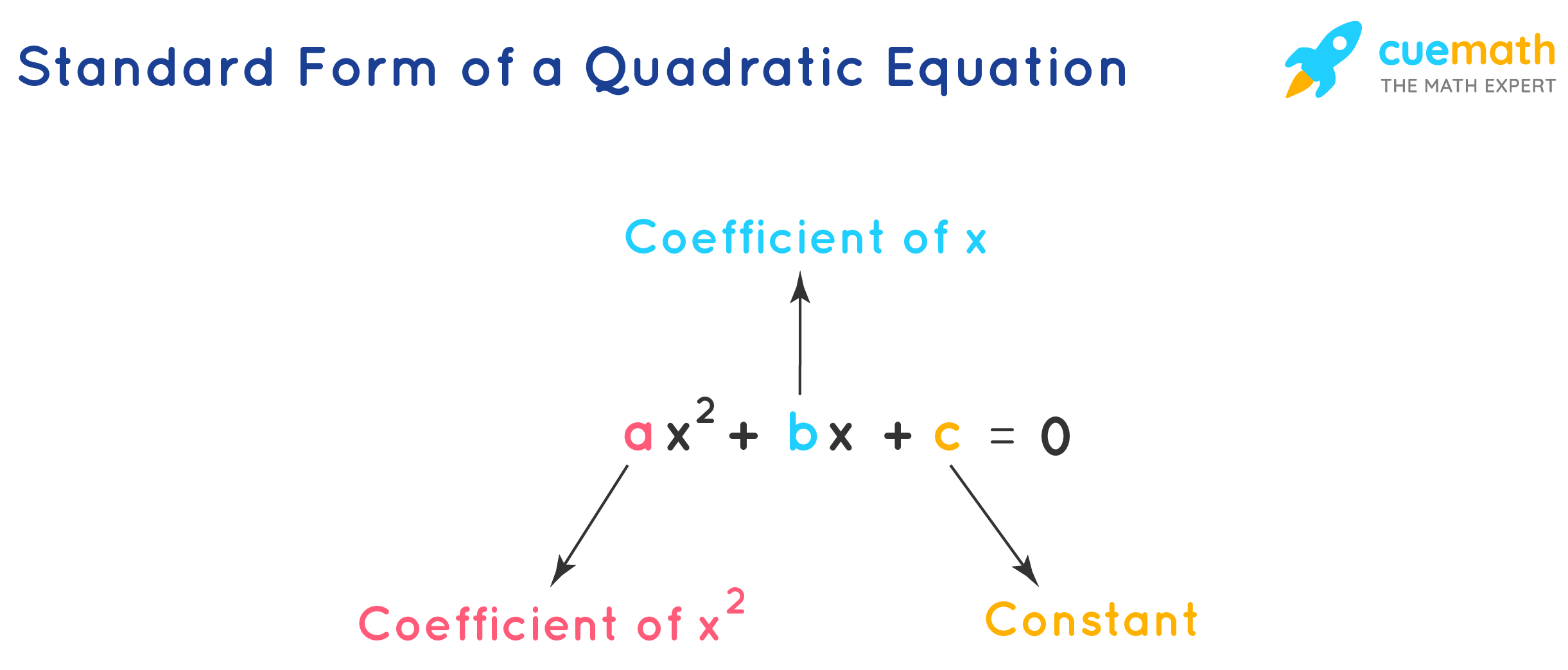
Further in real math issues the quadratic equations are presented in different forms: (x - ane)(x + 2) = 0, -x² = -3x + 1, 5x(10 + 3) = 12x, x³ = x(x² + x - 3). All of these equations demand to be transformed into standard class of the quadratic equation before performing farther operations.

Quadratic Equation Formula

Quadratic Formula is the simplest style to find the roots of a quadratic equation. There are certain quadratic equations that cannot be hands factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way. The roots of the quadratic equation further help to find the sum of the roots and the product of the roots of the quadratic equation. The 2 roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign tin be alternatively used to obtain the two distinct roots of the equation.

Quadratic Formula = [-b ± √(b² - 4ac)]/2a

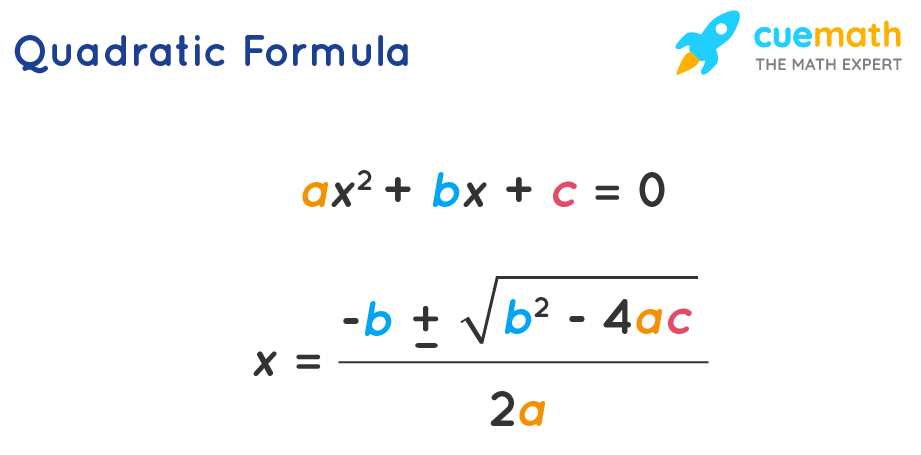
Important Formulas for Solving Quadratic Equations

The post-obit list of of import formulas is helpful to solve quadratic equations.

• The quadratic equation in its standard form is axⁱⁱ + bx + c = 0
• The discriminant of the quadratic equation is D = b² - 4ac
• For D > 0 the roots are real and distinct.
• For D = 0 the roots are existent and equal.
• For D < 0 the roots do non exist, or the roots are imaginary.
• The formula to notice the roots of the quadratic equation is 10 = \( \frac{-b \pm\sqrt{b^ii - 4ac}}{2a}\).
• The sum of the roots of a quadratic equation is α + β = -b/a = - Coefficient of x/ Coefficient of ten².
• The product of the Root of the quadratic equation is αβ = c/a = Constant term/ Coefficient of ten²
• The quadratic equation having roots α, β, is xⁱⁱ - (α + β)10 + αβ = 0.
• The condition for the quadratic equations \(a_1x^2 + b_1x + c_1 = 0\), and \(a_2x^ii + b_2x + c_2 = 0\) having the same roots is \(\dfrac{(a_1b_2 - a_2b_1)}{(b_1c_2 - b_2c_1)}\) = \((a_2c_1 - a_1c_2)^2\).
• For positive values of a (a > 0), the quadratic expression f(ten) = ax^two + bx + c has a minimum value at x = -b/2a.
• For negative value of a (a < 0), the quadratic expression f(10) = ax² + bx + c has a maximum value at x = -b/2a.
• For a > 0, the range of the quadratic equation axⁱⁱ + bx + c = 0 is [bⁱⁱ - 4ac/4a, ∞)
• For a < 0, the range of the quadratic equation ax² + bx + c = 0 is : (∞, -(b^two - 4ac)/4a]

Quadratic Formula Proof

Consider an arbitrary quadratic equation: ax^two + bx + c = 0, a ≠ 0

To make up one's mind the roots of this equation, nosotros proceed equally follows:

ax² + bx = -c ⇒ xⁱⁱ + bx/a = -c/a

Now, we limited the left mitt side as a perfect square, by introducing a new term (b/2a)² on both sides:

x²+ bx/a + (b/2a)² = -c/a + (b/2a)ⁱⁱ

The left mitt side is now a perfect foursquare:

(x + b/2a)² = -c/a + b^two/4a² ⇒ (ten + b/2a)² = (b² - 4ac)/4aⁱⁱ

This is good for united states, considering at present nosotros tin can take foursquare roots to obtain:

x + b/2a = ±√(b² - 4ac)/2a

x = (-b ± √(b^two - 4ac))/2a

Thus, by completing the squares, we were able to isolate 10 and obtain the 2 roots of the equation.

Roots of a Quadratic Equation

The roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. The roots of a quadratic equation are referred to by the symbols blastoff (α), and beta (β). These roots of the quadratic equation are too called the zeros of the equation. Hither we shall learn more almost how to detect the nature of roots of a quadratic equation without really finding the roots of the equation. And also bank check out the formulas to find the sum and the product of the roots of the equation.

Nature of Roots of the Quadratic Equation

The nature of roots of a quadratic equation tin can be found without really finding the roots (α, β) of the equation. This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The value b^two - 4ac is called the discriminant of a quadratic equation, and is designated as 'D'. Based on the discriminant value the nature of the roots of the quadratic equation can be predicted.

Discriminant: D = b² - 4ac

• D > 0, the roots are real and distinct
• D = 0, the roots are existent and equal.
• D < 0, the roots do not exist or the roots are imaginary.

Relationship Between Coefficients and Roots of Quadratic Equation

The coefficient of x², ten term, and the constant term of the quadratic equation ax² + bx + c = 0 are useful to study more nigh the properties of roots of the quadratic equation. The sum and production of roots of a quadratic equation tin can be direct calculated from the equation, without really finding the roots of the quadratic equation. The sum of the roots of the quadratic equation is equal to the negative of the coefficient of x divided by the coefficient of tenⁱⁱ. The product of the root of the equation is equal to the constant term divided by the coefficient of the 10². For a quadratic equation ax² + bx + c = 0, the sum and production of the roots are equally follows.

• Sum of the Roots: α + β = -b/a = - Coefficient of ten/ Coefficient of x²
• Production of the Roots: αβ = c/a = Abiding term/ Coefficient of ten²

The quadratic equation tin can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is every bit follows.

x² - (α + β)x + αβ = 0

Methods to Solve Quadratic Equations

A quadratic equation tin exist solved to obtain two values of x or the two roots of the equation. There are four different methods to find the roots of the quadratic equation. The four methods of solving the quadratic equations are equally follows.

• Factorizing of Quadratic Equation
• Formula Method of Finding Roots
• Method of Completing the Square
• Graphing Method to Find the Roots

Allow us look in item at each of the above methods to understand how to employ these methods, their applications, and their uses.

Factorization of Quadratic Equation

Factorization of quadratic equation follows a sequence of steps. For a general form of the quadratic equation ax² + bx + c = 0, we need to get-go split the middle term into two terms, such that the product of the terms is equal to the constant term. Further, we tin take the mutual terms from the bachelor term, to finally obtain the required factors. For understanding factorization, the general form of the quadratic equation can be presented equally follows.

• x² + (a + b)10 + ab = 0
• x² + ax + bx + ab = 0
• x(x + a) + b(x + a)
• (ten + a)(x + b) = 0

Let us understand factorization through the below instance.

• x² + 5x + 6 = 0
• ten^two + 2x + 3x + half dozen = 0
• 10(ten + 2) + 3(10 + 2) = 0
• (x + 2)(x + 3) = 0

Thus the two obtained factors of the quadratic equation are (x + 2) and (ten + 3).

Quadratic Formula to Discover Roots

The quadratic equations which cannot be solved through the method of factorization can be solved with the help of a formula. The formula to solve the quadratic equation uses the terms from the standard form of a quadratic equation. Through the below formula nosotros can obtain the 2 roots of x past first using the positive sign in the formula and and then using the negative sign. Whatsoever quadratic equation can exist solved using this formula.

Further to the above-mentioned ii methods of solving quadratic equations, in that location is another important method of solving a quadratic equation. The method of completing the square for a quadratic equation is as well useful to discover the roots of the equation. This method includes numerous algebraic calculations and hence has been explained as a separate topic.

Method of Completing the Square

The method of completing the square for a quadratic equation, is to algebraically foursquare and simplify, to obtain the required roots of the equation. Consider a quadratic equation ax² + bx + c = 0, a ≠ 0. To determine the roots of this equation, we simplify it every bit follows:

• axⁱⁱ + bx + c = 0
• ax² + bx = -c
• 10² + bx/a = -c/a

Now, we limited the left paw side as a perfect square, by introducing a new term (b/2a)ⁱⁱ on both sides:

• 10² + bx/a + (b/2a)² = -c/a + (b/2a)ⁱⁱ
• (ten + b/2a)² = -c/a + b²/4a²
• (x + b/2a)² = (b² - 4ac)/4a^two
• x + b/2a = +√(b²- 4ac)/2a

At present with this method of completing the square, we could consolidate the value for the roots of the equation. Further on simplification and taking the square root, the two possible roots of the quadratic equation are, x = (-b + √(b²- 4ac))/2a. Here the '+' sign gives i root and the '-' sign gives another root of the quadratic equation. More often than not, this detailed method is avoided, and but the formula is used to obtain the required roots.

Graphing a Quadratic Equation

The graph of the quadratic equation ax² + bx + c = 0 tin can be obtained by representing the quadratic equation as a part y = ax² + bx + c. Further on solving and substituting values for x, we can obtain values of y, we can obtain numerous points. These points can be presented in the coordinate axis to obtain a parabola-shaped graph for the quadratic equation.

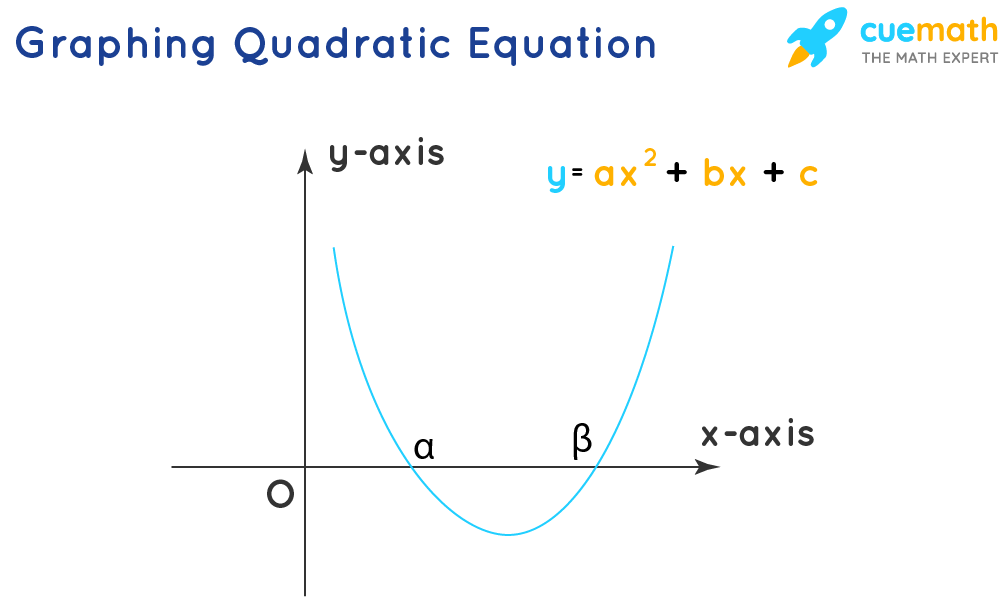
The indicate where the graph cuts the horizontal x-axis is the solution of the quadratic equation. These points can besides be algebraically obtained by equalizing the y value to 0 in the function y = ax² + bx + c and solving for x.

Quadratic Equations Having Common Roots

The ii quadratic equation having common roots are \(a_1x^ii + b_1x + c_1 = 0\), and \(a_2x^2 + b_2x + c_2 = 0\). Allow u.s.a. solve these ii equations to notice the conditions for which these equations have a common root. The two equations are solved for 10^two and x respectively.

\(\dfrac{ten^2}{(b_1c_2 - b_2c_1)}\) = \(\dfrac{-ten}{(a_1c_2 - a_2c_1)}\) = \(\dfrac{1}{(a_1b_2 - a_2b_1)}\)

\(x^2 =\dfrac{(b_1c_2 - b_2c_1)}{(a_1b_2 - a_2b_1)}\)

\(x=\dfrac{(a_2c_1 - a_1c_2)}{(a_1b_2 - a_2b_1)}\)

Hence of simplifying the higher up two expressions we take the following condition for the the two equations having the common root.

\(\dfrac{(a_1b_2 - a_2b_1)}{(b_1c_2 - b_2c_1)}\) = \((a_2c_1 - a_1c_2)^2\)

Maximum and Minimum Value of Quadratic Expression

The maximum and minimum value for the quadratic equation ax² + bx + c = 0 tin be observed in the below graphs. For positive values of a (a > 0), the quadratic expression has a minimum value at x = -b/2a, and for negative value of a (a < 0), the quadratic expression has a maximum value at x = -b/2a.

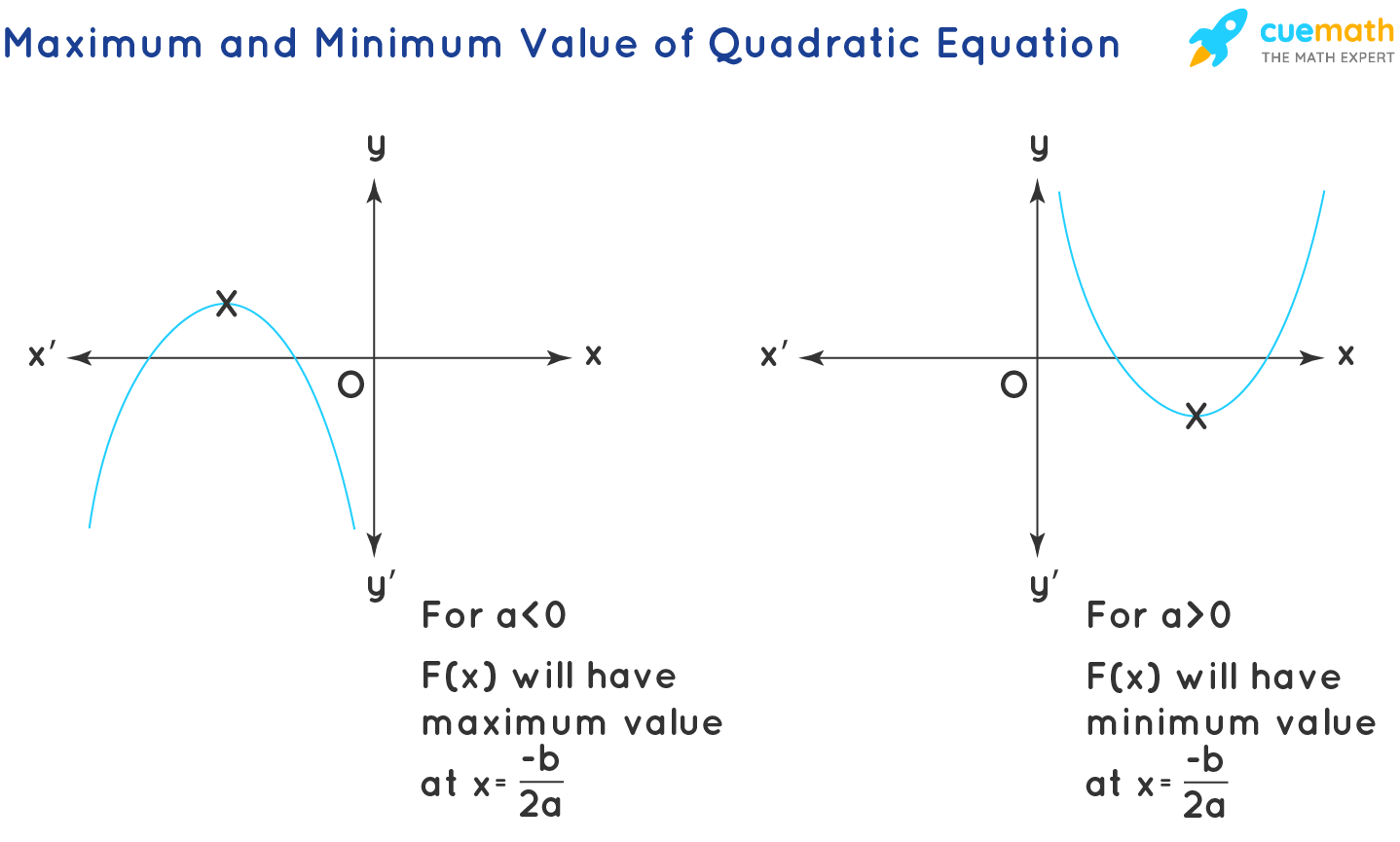
The maximum and minimum values of the quadratic expressions are of farther help to find the range of the quadratic expression: The range of the quadratic expressions as well depends on the value of a. For positive values of a( a > 0), the range is [ f(-b/2a), ∞), and for negative values of a ( a < 0), the range is (-∞, f(-b/2a)].

• For a > 0, Range: [ f(-b/2a), ∞)
• For a < 0, Range: (-∞, f(-b/2a)]

Solving a Quadratic Equation - Tips and Tricks

Some of the below-given tips and tricks on quadratic equations are helpful to more easily solve quadratic equations.

1. The quadratic equations are generally solved through factorization. Just in instances when it cannot exist solved by factorization, the formula is used.
2. The roots of a quadratic equation are also called the zeroes of the equation.
3. For quadratic equations having negative discriminant values, the roots are represented with the help of circuitous numbers.
4. The sum and product of roots of a quadratic equation tin can be used to observe higher algebraic expressions involving these roots.

Related Topics

• Zeroes and Roots
• Nature of Roots - Examples
• Square Root
• Roots Calculator
• Factorization of Quadratic Equations
• Sum and Production of Roots
• Weather on Roots of Quadratics
• Roots of Quadratic Equation Calculator

Examples on Quadratic Equations

1. Example 1: Meghan is a fitness enthusiast and goes for a jog every morning time. The park where she jogs is rectangular in shape and measures 12m × 8m. An environmentalist group plans to revamp the park and decides to build a pathway surrounding the park. This would increase the total area to 140 sq m. What will exist the width of the pathway?

   Solution:

   Let's denote the width of the pathway by x.

   So, the length and breadth of the outer rectangle is (12+2x) m and (8+2x) one thousand.

   According to the question,

   (12 + 2x)(8 + 2x) = 140

   2(6 + x) 2(4 + x) = 140

   (6 + x)(4 + x) = 35

   24 + 6x + 4x + x^two = 35

   xⁱⁱ + 10x -11 = 0

   x² + 11x - x - 11 = 0

   x(10 + eleven) - 1(x + 11) = 0

   (10 + 11)(x - 1) = 0

   (10 + 11) =0 and (x - 1) = 0

   x = -11 and x = ane

   Since length can't exist negative, nosotros take x = one.

   Respond: Therefore the width of the pathway is 1m.

2. Example 2: Permit's learn how a quadratic equation question finds its awarding in the field of move. Rita throws a ball upwards from a platform that is 20m in a higher place the ground. The height of the ball from the ground at a time 't', is denoted past 'h'. Suppose h = -4t^two + 16t + xx. Detect the maximum acme attained by the ball.

   Solution:

   We tin rearrange the terms of the quadratic equation

   h = -4t² + 16t + twenty

   in such a mode that it is easy to find the maximum value of this equation.

   h = -4t² + 16t + 20

   = -4t² + 16t + xx

   = -4(t^two - 4t - five)

   = -4((t - ii)² - 9)

   = -4(t - 2)² + 144

   We should proceed the value of (t-2)^two minimum in club to find the maximum value of h.

   So, the minimum value (t-2)ⁱⁱ can accept is 0.

   Answer: Therefore the maximum height attained is 144m.

3. Example 3: Find the quadratic equation having the roots 5 and 8 respectively.

   Solution:

   The quadratic equation having the roots α, β, is x² - (α + β)x + αβ = 0.

   Given α = 5, and β = 8.

   Therefore the quadratic equation is:

   x² - (v + 8)x + five×8 = 0

   ten^two - 13x + 40 = 0

   Answer: Hence the required quaratic equation is x^two - 13x + 40 = 0

4. Example 4: The quadratic equation 2x² + 9x + 7 = 0 has roots α, β. Find the quadratic equation having the roots 1/α, and 1/β.

   Solution:

   The quadratic equation having roots that are reciprocal to the roots of the equation axⁱⁱ + bx + c = 0, is cx² + bx + a = 0.

   The given quadratic equation is 2xⁱⁱ + 9x + 7 = 0.

   Hence the required equation having reciprocal roots is 7x² + 9x + 2 = 0.

   Answer: Therefore the equation is 7x² + 9x + 2 = 0.

go to slidego to slidego to slidego to slide

Breakdown tough concepts through simple visuals.

Math volition no longer be a tough discipline, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Practice Questions on Quadratic Equations

go to slidego to slide

FAQs on Quadratic Equation

What is a Quadratic Equation?

A quadratic equation in math is a second-caste equation of the course ax² + bx + c = 0. Here a, b, are the coefficients, c is the constant term, and 10 is the variable. Since the variable x is of the 2d degree, at that place are two roots or answer for this quadratic equation. The roots of the quadratic equation tin be constitute by either solving by factorizing or through the use of a formula.

What is the Quadratic Formula?

The quadratic formula to solve a quadratic equation ax² + bx + c = 0 is 10 = [-b ± √(b² - 4ac)]/2a. Hither we obtain the 2 values of x, by applying the plus and minus symbol in this formula. Hence the two possible values of 10 are [-b + √(b² - 4ac)]/2a, and [-b - √(b² - 4ac)]/2a.

How to Utilize Quadratic Formula?

The values of a, b, and c are practical to the quadratic formula x = [-b ± √(b² - 4ac)]/2a, to obtain the two roots of the quadratic equation.

What is Determinant in Quadratic Formula?

The value b² - 4ac is called the determinant and is designated as D. The determinant is role of the quadratic formula. The determinants aid u.s.a. to notice the nature of the roots of the quadratic equation, without actually finding the roots of the quadratic equation.

What are Some Real Life Applications of Quadratic Equations

Quadratic equations are used to find the zeroes of the parabola and its axis of symmetry. There are many real-world applications of quadratic equations. For instance, information technology tin can be used in running time issues to evaluate the speed, distance or time while traveling past auto, train or airplane. Quadratic equations draw the relationship between quantity and the cost of a commodity. Similarly, demand and cost calculations are also considered quadratic equation problems. It can likewise be noted that a satellite dish or a reflecting telescope has a shape that is defined by a quadratic equation.

How are Quadratic Equations Different From Linear Equations?

A linear degree is an equation of a single degree and one variable, and a quadratic equation is an equation in two degrees and a single variable. A linear equation is of the the class ax + b = 0 and a quadratic equation is of the grade ax² + bx + c = 0. A linear equation has a single root and a quadratic equation has two roots or two answers. Also, a quadratic equation is a product of two linear equations.

How to Simplify a Quadratic Equation?

The first stride in the process of simplifying a quadratic equation is to transform information technology into the standard class ax² + bx + c = 0. Farther, information technology can be simplified by finding its factors through the process of factorization. Also for an equation for which it is difficult to factorize, it is solved by using the formula. Additionally, there are a few other ways of simplifying a quadratic equation.

What Are the 4 Ways To Solve A Quadratic Equation?

The 4 ways of solving a quadratic equation are as follows.

• Factorizing method
• Formula Method
• Method of Completing Squares
• Graphing Method

How Practice y'all Solve a Quadratic Equation Past Factoring?

The quadratic equation tin can exist solved by factorization through a sequence of three steps. First split the middle term, such that the product of the split terms is equal to the product of the first and the last terms. Permit us assume the quadratic equation is of the form x² + (a + b)x + ab = 0, and it tin be split as x² + ax + bx + ab = 0. As a second footstep, take the common term from the first two and the last two terms. x(x + a) + b(x + a) = 0, (ten + a)(10 + b) = 0. Finally equalize each of the factors to nix and obtain the ten values. x + a = 0 and x + b = 0, and hence we tin can obtain x = -a and x = -b

How to Solve a Quadratic Equation by Completing the Square?

The quadratic equation solved by the method of completing the square and it uses the formula (a + b)² = a²

How to Find the Value of the Discriminant?

The value of the discriminant in a quadratic equation can be institute from the variables and constant terms of the standard class of the quadratic equation ax² + bx + c = 0. The value of the discriminant is D = b² - 4ac, and it helps to predict the nature of roots of the quadratic equation, without actually finding the roots of the equation.

How Do Yous Solve Quadratic Equations With Graphing?

The quadratic equation can be solved similarly to a linear equal by graphing. Let us take the quadratic equation ax² + bx + c = 0 as y = ax² + bx + c . Here we take the set of values of 10 and y and plot the graph. These two points where this graph meets the 10-axis, are the possible solutions of this quadratic equation.

How To Notice Nature of Roots of Quadratic Equation?

The discriminant is helpful to predict the nature of the roots of the quadratic equation. The determinant of a quadratic equation ax² + bx + c = 0 is b² - 4ac. The discriminant is referred as D = b² - 4ac. If D > 0 the roots are real and singled-out, for D = 0 the roots are equal, and for D < 0 the roots are imaginary complex numbers.

How Important Is the Discriminant in Determining the Nature of Roots of Quadratic Equation?

The discriminant is very much needed to easily notice the nature of roots of the quadratic equation. Without the discriminant, finding the nature of the roots of the equation is a long process, as we first demand to solve the equation to find both the roots. Hence the discriminant is an important and the needed quantity, which helps to easily find the nature of roots of the quadratic equation.

When Do Quadratic Equations Have Equal Roots?

The given quadratic equation has equal roots if the discriminant is equal to nil. For a quadratic equation of the course ax² + bx + c = 0 the discriminant is D = b² - 4ac = 0. Here both are roots are equal and each has a value of ten = -b/2a.

What is the Employ of Determinants in Quadratic Formula?

The determinant (D = b² - 4ac) is useful to predict the nature of the roots of the quadratic equation. For D > 0, the roots are real and distinct, for D = 0 the roots are real and equal, and for D < 0, the roots do not exist or the roots are imaginary complex numbers. With the help of this determinant and with the least calculations, we tin can detect the nature of the roots of the quadratic equation.

How Many Roots does Quadratic Equation Accept?

It is a 2nd-degree equation in x, and hence two roots are obtained. We tin can obtain these roots of a quadratic equation using the quadratic formula. One root tin be obtained using the positive sign and we can become another root past applying the negative sign in the formula.

How exercise you Solve a Quadratic Equation without Using the Quadratic Formula?

There are two alternative methods to the quadratic formula. One method is to solve the quadratic equation through factorization, and another method is by completing the squares. In full there are three methods to find the roots of a quadratic equation.

How is Quadratic Formula used to Solve a Quadratic Equation?

The algebra formula (a + b)² = a² + 2ab + b² is used to solve the quadratic equation and derive the quadratic formula. This algebraic formula is used to manipulate the quadratic equation and derive the quadratic formula to find the roots of the equation.

abbotttheming.blogspot.com

Source: https://www.cuemath.com/algebra/quadratic-equations/

Share this post